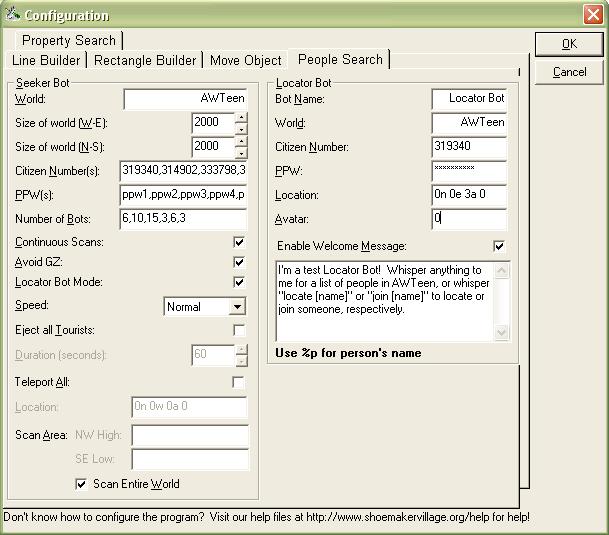
Figure 5: The People Search function correctly configured as explained below.
Finding People
The People Search function of the Activeworlds Utility allows a user to search a world to locate all users within a specific area.

Figure 5: The People Search function correctly configured as explained below.
While the myriad of options available might seem intimidating at first, most are optional and can be ignored by all except experienced users.
The People Search function of the utility works by sending an array of bots to move through a world in a "grid" pattern. As the bots move through the world, they do so at a very fast speed, which is usually fast enough to be unnoticeable by human observers somewhere in the world. However, as each bot "sweeps" through an area and detects a person, it is added to a list of "found" people. You can then determine the user's location and perform a variety of actions, such a teleporting to a person, moving a person elsewhere in the world, ejecting the user, and so on. The bots that sweep the world are referred to as "Seeker Bots." Locator bots add another level of functionality to the people search, which is explained later.
For now, enter the name of the world that you wish to search under the "World" option in the Seeker Bot frame. The boundaries of the world are simply the number of coordinates the buildable area of the world extends from ground zero. For example, a p-50 world extends 50 coordinates from ground zero, so the maximum coordinates in both directions would be 50 for that type of world. In the case above, the bots are searching AWTeen, which extends 2000 coordinates in each direction.
Next, enter your citizen number in the box below, or the citizen number of the account you wish to use. Enter your privilege password in the next box, and the number of bots in the third box. For most accounts, the maximum number of bots that can be used is three, but this number can be raised or lowered depending on whether bots are in use, whether you've won or paid for a bot limit increase, or by a variety of other means. The more bots that are used, the less time that is taken during the search.
For Advanced Users: As in the picture above, it is possible to specify multiple citizen accounts in order to increase the number of bots you can use to scan a world simultaneously. To use more than one account, separate the citizen information by commas. The privilege passwords and numbers of bots correspond to the number of commas before the citizen number. For example, in the dialog above, citizen 319340's privilege password is "ppw1," and the number of bots that account uses is 6. Citizen 314902 uses 10 bots and has privilege password "ppw2," and so on. Be careful - if you miss entering a comma or enter more privilege passwords than citizen numbers or vice-versa, you will receive a message to recheck the citizen info you entered.
Several more options are displayed in checkboxes below the citizen number dialog boxes. The "continuous scans" option simply specifies whether you would like scanning of the world to continue after the first "sweep" is complete. By default, this option is unchecked, and the area you specify will be scanned once, after which scanning will stop. If you specify that you would like continuous scans, the Seeker Bots will continue searching the world until you lose your Internet connection or you tell the bots to stop by pressing CTRL-S.
Selecting the Avoid GZ option allows you to instruct all of the bots to avoid the ground zero area of the world you specify. This is most useful in worlds that disallow bots near GZ. For example, the [Customs Aide] bot in most AWC-owned worlds will eject all bots near GZ, including the Seeker Bot that moves through GZ in an attempt to locate avatars. To avoid ejection, check the "Avoid GZ" option to prevent Seeker Bots from moving through ground zero. Note, however, that citizens near ground zero won't be detected in this case.
The Locator Bot Mode checkbox will be explained in the next topic.
The Speed combo box allows you to specify the speed at which the Seeker Bots sweep through the world. For most users, this option can be set at Normal for a trouble-free run at 100% accuracy. However, users with low ping times and fast world servers may wish to try increasing the speed at which the Seeker Bots sweep the world searching for avatars. In most cases, however, increasing the speed will decrease the bots' accuracy, so changing this option is not recommended.
The option to eject all tourists which are encountered is provided and may be useful for owners of worlds that prohibit tourist entry, or who are inflicted with vandalism cases caused by tourists who wish to remain anonymous. When this option is checked, you may specify the number of seconds for tourists to be ejected each time they are encountered by a Seeker Bot.
Another useful feature enables the ability to teleport all users encountered to a specific location. For example, you might wish to teleport all users in your world to a specific location immediately before an event. This option is most useful when the Seeker Bots are not set to "continuous scan" mode, because users will be unable to move if they are constantly teleported by continually scanning Seeker Bots. You can specify the location (in normal AW coordinates) to which you would like to teleport users in the "Location" text box.
Finally, the "Scan Entire World" checkbox allows you to specify whether the entire world you specify is scanned. If you uncheck this box, specify the northwest and southeast corners of the area which you would like to scan. If you enter invalid coordinates, or the southeast corner is further north or west than the northwest corner, an error occurs.
Next Topic: The Locator Bot
Previous Topic: Moving Objects
Back to Menu